سلام به همه ی ریاضی دوستان وتیزهوشان امیدوارم لذت ببرید
معلم گرامی :جناب آقای امین جهانگیری
- وضعیت پیشرفت دانش آموزانتان را زیر نظر بگیرید .
- رتبه بندی دانش آموزان را در لحظه ببینید .
- حضور و غیاب ها را ثبت کنید .
- بودجه بندی اصلی را با بودجه بندی طی شده مقایسه کنید .
- برنامه هفتگی کلاس هایتان را وارد کنید .
- تمام درس های تان را یک جا مدیریت کنید .(پشتیبانی از چندین درس)
- از عملکرد دانش آموزان گزارش تهیه کنید .
- نمرات را ثبت کنید و ریز نمرات ثبت شده را همراه با موضوع و تاریخ ثبت مشاهده کنید .
- اسامی دانش آموزان را از سامانه سناد وارد کنید .
.:: اپلیکیشن کلاس من با آندروید 4 و بالاتر سازگار است ::.
Algebrator نرم افزار فوق العاده ای است که در یادگیری ریاضیات و حل معادلات پیچیده ای که ممکن است بسیاری از دانش آموزان در آن مشکل داشته باشند، بسیار مفید واقع شده است. شما با کمک این نرم افزار قادر خواهید بود معادلات مطرح شده در مبحث های مختلف ریاضیات مانند معادلات، انتگرال گیری، بررسی توابع، ریشه یابی، لگاریتم، ماتریس، توابع مثلثاتی و ... را نوشته و حل نمایید. Algebrator مهارت شما را در حل تمرینات دشوار بالا برده تا قادر باشید سخت ترین مسائل ریاضی را به آسانی حل کنید و اگر از درسی عقب مانده اید یا آن را بخوبی متوجه نشده اید، پاسخ تشریحی تمام سوالات خود را ریز به ریز و مرحله به مرحله از این برنامه دریافت کنید.
برای تمام سنین
نرم‌افزار Algebrator برنامه‌ای با روش کار بسیار ساده است که شما را قادر می‌سازد در هر سن و هر مقطعی که باشید سوالات ریاضی خود را به آسانی حل کنید! اگر فرزندانتان از شما سوالاتی می‌کنند که قادر به حل آنها نیستید یا اگر خودتان مشغول تحصیل هستید و به دنبال راه‌حل و پاسخ یک سوال پیچیده می‌گردید، براحتی میتوانید با استفاده از این نرم‌افزار، پاسخ را در زمانی بسیار کوتاه مشاهده کنید. حتی اگر استاد دانشگاه باشید یا یک موسسه آموزشی را مدیریت می‌کنید و با مسائل پیچیده ریاضی سر و کار دارید، باز هم بدون نیاز به ماشین‌حساب‌های گران قیمت و صرف وقت طولانی برای حل مسائل ریاضی، میتوانید در مدت زمانی بسیار کوتاه صورت مساله را در این نرم‌افزار تعریف و پاسخ را در کسری از ثانیه مشاهده کنید!
پاسخ‌های کاملا تشریحی
نرم‌افزار Algebrator در عین حال که قادر است پاسخ مسائل را در کسری از ثانیه در اختیار شما قرار دهد، به‌گونه‌ای طراحی شده است که پاسخ تشریحی بسیار کاملی را از مراحل حل مساله در اختیار شما قرار می‌دهد. به‌این ترتیب چگونگی حل هیچ‌یک از مسائل برای شما ابهام نخواهد داشت و به‌طور کامل میتوانید مساله و روش حل آن را درک کنید.
قابلیت های کلیدی نرم افزار Algebrator:
ـ حل انواع مسائل ریاضی در تمام مقاطع تحصیلی
ـ حل مسائل با استفاده از روش‌های معمول و رایج بین‌المللی
ـ ارائه پاسخ تشریحی مرحله به مرحله همراه با پشتیبانی از قابلیت راهنمایی و آموزش قوانین، قضایا و پیش‌نیازهای حل یک مساله
ـ رسم انواع نمودار و گراف‌های مربوط در کوتاه‌ترین زمان ممکن
ـ پشتیبانی از ویرایشگر قدرتمند WYSIWYG برای نوشتن صورت مساله
ـ انتشار مساله و روش حل آن در فرمت استاندارد به‌صورت یک فایل xhtml قابل مشاهده در تمام مرورگرهای وب
ـ پشتیبانی از حل مسائل با تعداد ارقام بالا
و...
فقط سوم راهنمایی ها بخوانند
یکی از مشکلاتی که نوعاً دانش‌آموزان با آن مواجه هستند، حلّ مسأله‌های مربوط به تناسب است به طوری که گاهی تغییری در صورت مسأله ممکن است حلّ آن را برای دانش‌آموز غیرممکن سازد.
در این جا با طرح مسأله‌های کار و کارگر سعی داریم تا این مشکل را برطرف سازیم.
مسأله‌ی اوّل: M کارگر کاری را در D روز انجام می‌دهند. اگر پس از گذشت d روز m کارگر (m < M , d < D) قادر به ادامه‌ی کار نباشند. کار چند روزه تمام خواهد شد؟[فرض بر این است که تمام کارگر‌ها در هر روز به طور مساوی کار می‌کنند و خروج تعدادی از کارگران از کار، تأثیری بر میزان کار بقیه ی کارگران نمی‌گذارد.]
حلّ: اگر میزان کلّ کار را 1 واحد بگیریم، پس هر کارگر به میزان 
واحد کار در روز بایستی انجام دهد. میزان کاری که M کارگر در d روز انجام می‌دهند برابر است با:
.
اگر پس از خروج m کارگر از کار، ادامه‌ی کار 
روز طول بکشد آن‌گاه میزان کاری که M-m کارگر درروز انجام می‌دهند برابر است با:
.
چون کلّ کار 1 واحد است، لذا خواهیم داشت:
و لذا خواهیم داشت:
. اگر فرض کنیم پس از خروج m کارگر، کار در
روز به اتمام خواهد رسید آن‌گاه:
.
مثال: 21 کارگر کاری را در 12 روز تمام می‌کنند، اگر پس از گذشت 6 روز، 3 کارگر بیمار شوند، کار چند روزه تمام خواهد شد؟ حلّ: 21=M و 12=D و 6=d و 3=m . بنابراین:
.
مسأله‌ی دوّم: اگر در مسأله‌ی اوّل به جای عبارت: "پس از گذشت d روز" عبارت: "پس از انجام 
کار (1 < K)" را بیاوریم؛ مسأله چگونه حلّ می‌شود؟
حلّ: اگر پس از خروج m کارگر از کار، ادامه‌ی کار روز طول بکشد آن‌گاه میزان کاری که M-m کارگر در روز انجام می‌دهند برابر است با:
و چون کار پیش از خروج m کارگر انجام شده است لذا داریم:
.
اگر فرض کنیم پس از خروج m کارگر، کار در روز به اتمام خواهد رسید آن‌گاه:
که در آن 
زمان لازم برای انجام واحد کار است.
مثال: 10 کارگر کاری را در 30 روز انجام می‌دهند. اگر پس از انجام ثلث کار، 5 کارگر بیمار شوند، کار چند روزه تمام خواهد شد؟
حلّ: 10=M و 30=D و 3=K و 5=m .بنابراین:
مسأله‌ی‌سوّم: M کارگر N هکتار زمین را در D روز شخم می‌زنند. 
کارگر(M>) ، 
هکتار زمین(N<) را در چند روز شخم می‌زنند؟ [فرض مسـأله ی اوّل برقرار است.]
حلّ: میزان کاری که هر کارگر در طول روز انجام می‌دهد عبارت است از
. اگر کارگر هکتار زمین را در روز شخم بزنند آن‌گاه:
.
مثال: 20 کارگر، 12 هکتار زمین را در 6 روز شخم می‌زنند. 15 کارگر، 18 هکتار زمین را در چند روز شخم می‌زنند؟
اکنون پس از مطالعه‌ی مسائل و مثال‌های فوق، قادر خواهید بود تا آگاهانه‌تر از رابطه‌های مربوط به مبحث تناسب معکوس استفاده نمائید و به روشی برای حلّ این گونه مسائل دست یافته‌اید.
برای گرفتن سوالات روی لینکهای زیر کلیک نمایید:
سوالات ورودی دبیرستان انرژی اتمی سال 1389
پاسخ سوالات ورودی دبیرستان انرژی اتمی سال 1389
سوالات و پاسخ ورودی دبیرستان انرژی اتمی سال 1390
سوالات ورودی دبیرستان انرژی اتمی سال 1391
دانلود پاورپوینت های آموزش رسم های کتاب درسی پایه های 1 ، 2 و 3 راهنمایی .
اهرم ها
بر حسب این که تکیه گاه بین نیروی محرک و نیروی مقاوم دقیقأ کجا قرار گیرد که خود سه حالت دارد.
حالت اول:
اگر تکیه گاه درست وسط دو نیرو قرار بگیرد ، طول بازوی محرک و مقاوم برابر می شوند. پس این اهرم غیر از انتقال نیرو فقط با تغییر جهت نیرو به ما کمک می کند.
در این اهرم مزیت مکانیکی همیشه ۱ است مانند قرقره ثابت ،آلاکلنگ
حالت دوم:
اگر تکیه گاه به نیروی مقاوم نزدیکتر باشد ، در این حالت طول بازوی محرک بزرگتر از طول بازوی مقاوم می گردد ،پس با افزایش مقدار نیرو به ما کمک می کند . وقتی تکیه گاه مطابق شکل به وزنه نزدیک می کنید و تخته را به طرف پایین می کشید . در این حالت برای بلند کردن وزنه نیروی کمتری لازم خواهد بود، ولی وزنه هم مقداری کمی بالا می رود در حالی که دست های شما بیشتر پایین می آیند .مانند میخ کش وزمانی که تکیه گاه بین نیروی محرک و نیروی مقاوم ولی نزدیک به نیروی مقاوم باشد, در این حالت, اهرم از راه های زیر به ما کمک می کند.
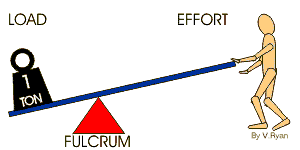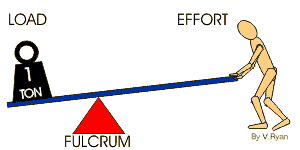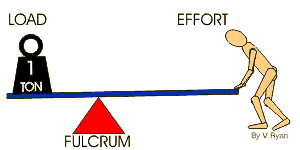
تغییر جهت نیرو: زیرا تکیه گاه بین نیروی محرک و مقاوم قرار دارد.
افزایش نیرو: زیرا بازوی محرک بزرگتر از بازوی مقاوم است. و مزیت مکانیکی این اهرم همواره از یک بیش تر است
حالت سوم:
اگر تکیه گاه به نیروی محرک نزدیک باشد ، طول بازوی مقاوم بزرگتر از طول محرک می شود ، پس در این حالت با افزایش مسافت و سرعت اثر نیرو بما کمک می کند. وقتی تکیه گاه را به محلی قرار دهید که به دستتان نزدیک باشد ، در این حالت برای بلند کردن وزنه باید نیروی زیادتری به کار ببرید ، ولی وزنه بیشتر بلند می شود در حالی که دستتان کمی به طرف پایین حرکت می کند. مانند قیچی کاغذ بری وزمانی که تکیه گاه بین نیروی محرک و نیروی مقاوم بوده ولی نزدیک به نیروی محرک باشد, در این حالت اهرم از راه های زیر به ما کمک می کند.
اهرم نوع دوم:
اهرمی گفته می شود که نیروی مقاوم آن بین تکیه گاه و نیروی محرک باشد. یعنی تکیه گاه در یک انتها ی اهرم بوده و نیروی مقاوم بین تکیه گاه و نیروی محرک قرار دارد . به عبارت دیگر در اهرم نوع دوم نیروی محرک در یکی از دو سراهرم قراردارد و نیروی مقاوم بین تکیه گاه ونیروی محرک قرار دارد .طول بازوی محرک همیشه با طول اهرم برابر است . پس فقط با افزایش مقدار نیرو به ما کمک می کند یعنی در نیروی محرک صرفه جویی می نماید.
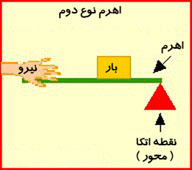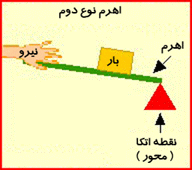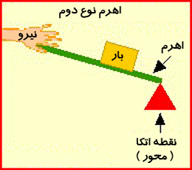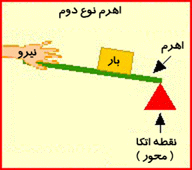
اهرم نوع دوم جهت نیرو را تغییر نمی دهد . زیرا جهت حرکت نیروی محرک و نیروی مقاوم رو به بالا است.
مزیت مکانیکی این اهرم همیشه از یک بیشتر است.
اهرم نوع دوم مانند :چرخ دستی -فرغون - فندق شکن،گیوتین کاغذ،پانچ-درب بطری باز کن و...
۱)تغییر جهت نیرو: زیرا تکیه گاه بین نیروی محرک و مقاوم قرار است.
افزایش مسافت اثر نیرو: زیرا بازوی مقاوم بزرگتر از بازوی محرک است. (LR>LE) و مزیت مکانیکی این اهرم همواره از یک کم تر است.
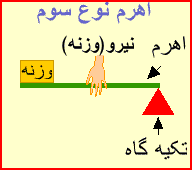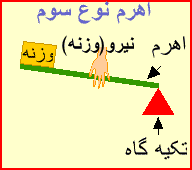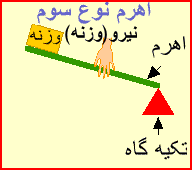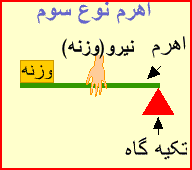
اهرم نوع سوم:
به اهرمی گفته می شود که نیروی محرک آن بین تکیه گاه و نیروی مقاوم باشدیعنی در اهرم نوع سوم نیروی مقاوم در یکی از دوسر اهرم ، ونیروی محرک بین نیروی مقاوم و تکیه گاه قرار دارد ، در این نوع، طول بازوی مقاوم همیشه با طول اهرم برابر است ،پس فقط با افزایش مسافت و سرعت اثر نیرو به ما کمک می کند یعنی در وقت صرفه جوئی می کند
مزیت مکانیکی آن کمتر از ۱ است
دانلود پاورپوینت زیبا از آتشفشان ها
دانلود پاورپینت جغرافی سوم راهنمایی
| لینک فایل | حجم فایل |
درس_دفاعی.  pptx |
82.179 KB |
برای دانش آموزان سال سوم راهنمایی
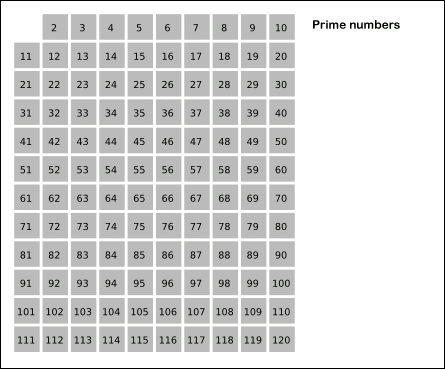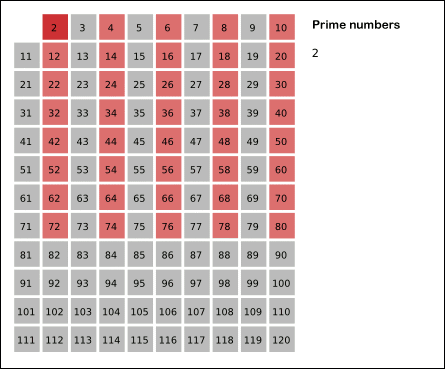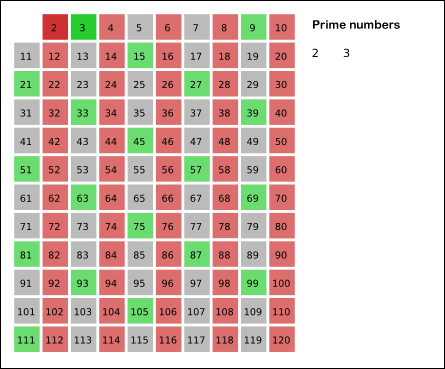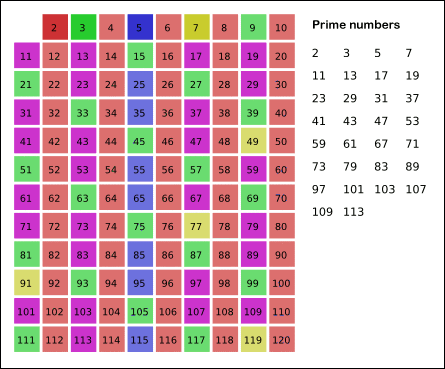
پاورپوینت الگوریتم غربال برای تعیین اعداد اول
محاسبه مقدار عددی یک عبارت جبری دانلود
حل معادله دانلود
خاصیت توزیع پذیری ضرب نسبت به جمع وتفریق دانلود
ضرب یک جمله ای در یک جمله ای دانلود
بازی ، سرگرمی ، هوش و دوران "
جهت دانلود نمونه سوالات موضوعی
و امتحانات نهایی درس ریاضی پایه ی سوم راهنمایی
و" یک منبع تمرینی خوب" اینجا کلیک کنید.
نکات طلایی ریاضی سوم برای آمادگی آزمون های ورودی
بازی درسی ریاضی شلیک به توان
حجم ۱ مگابایت
در این پست سعی بر این داریم تا برای فعالیت ها و کاردرکلاس های مندرج در فصل بردار و مختصات اسلایدهایی مخصوص تدریس در کلاس درس جهت استفاده دبیران محترم آماده و منتشر نمایم.
اسلایدهای فصل پنجم کتاب ریاضی پایه هشتم : بردار و مختصات
.:: لطفا در صورت مشاهده مشکل در اسلاید ها به ما اطلاع دهید تا به رفع آن بپردازیم ::.
ناشناس
